Lenses Archives - 1stVision Inc. - Machine Vision Articles

November 7, 2025November 12, 2025

VIS-SWIR solutions – the problems it solves

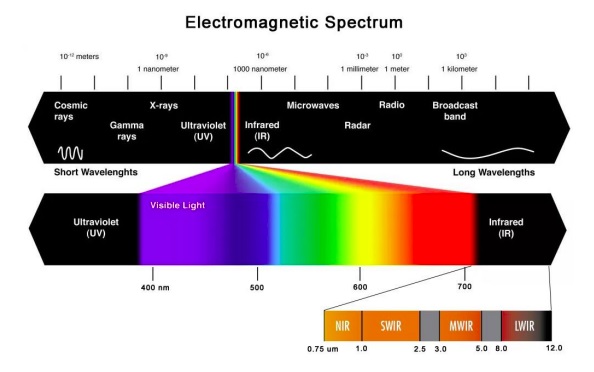
While we humans can only see what we’ve named to be visible light, bees can see UV light! Some camera sensors register IR wavelengths! Some cameras can sense both visible light and on through NIR and SWIR.

In this piece we focus on applications that benefit from combined VIS-SWIR solutions, from 400 nm through 2.5 nm.

Deconstructing the electromagnetic spectrum into it’s commonly known constituent regions

Example applications

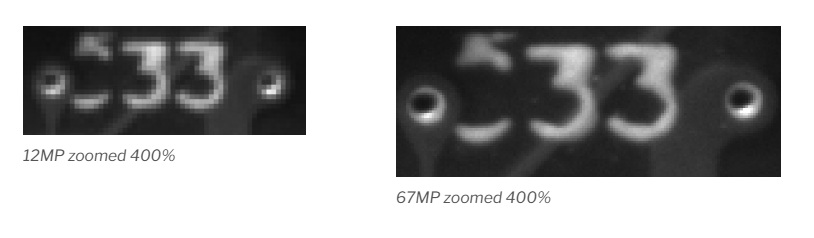
Just to whet the appetite, consider the 4 sets of image pairs below. In each case, the leftmost image was captured with visible wavelengths, while the righthand image utilized SWIR portions of the spectrum. These pairs were chosen to highlight the compelling power of SWIR to identify features that are not apparent in the visible portion of the spectrum.

VIS-SWIR image pairs – Courtesy Allied Vision – a TKH company

For certain applications, one wouldn’t need the human-visible images, of course, as with machine vision the whole point is to automate the image processing and corresponding actions. So for counterfeit banknote detection, bottle fill level monitoring, materials identification, or crop monitoring, one might just design for the SWIR portion of the spectrum and ignore the VIS.

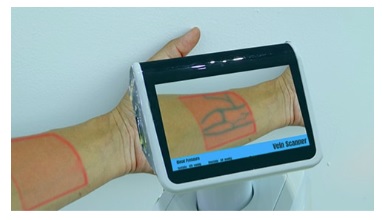
*Vein imaging application overlays SWIR image of veins into visible image of patient forearm –* *Image courtesy TAMRON*

But some applications might benefit from both the VIS and the SWIR images. For example, the vein imaging application might require a VIS reference image as well as a SWIR-specific image, for patient education and/or medical records.

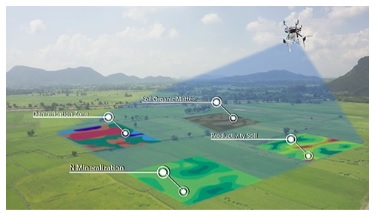
*Monitor moisture levels in crops from airborne drone – Image courtesy TAMRON*

For the crop monitoring application above, the VIS spectrum clearly orients trees, hills, buildings, and roadways. Meanwhile pseudo-color-mapping shows the varied moisture levels as sensed in the SWIR portion of the spectrum.

The range of potential applications combining VIS and SWIR is staggering. One can improved on one’s own or a competitor’s previous application. Or innovate something altogether new.

Sensors that register both VIS and SWIR wavelengths

Sony’s IMX992 and IMX993 sensors utilize Sony’s SenSWIR technology, such that a single sensor and camera may be deployed across the combined VIS and SWIR portions of the spectrum. Without such sensors, a VIS SWIR solution would require at least two separate cameras – one each for VIS and SWIR, respectively. That would add unnecessary expense, takes up more space, and require camera and image synchronization.

Now there are cameras, such as several in Allied Vision’s Alvium series, in which Sony’s SenSWIR sensors are embedded. With several interface options, including mipi, USB3 Vision, and 5GigE Vision:

Mipi, USB3 Vision, and 5GigE Vision interface options – Courtesy Allied Vision – a TKH Company

Lens manufacturers doing their part

One of the beauties of the free-market system, together with agreements on standards for interfaces and lens mounts, is that each innovator and manufacturer can focus on what he does best. Sensor manufacturers bring out new sensors. Camera designers embed those sensors and provide programming controls, communications interfaces, and lens mounts. And optics professionals design and produce lenses. The benefits from a range of choices, performance options, and price points.

Navitar VIS-SWIR lenses

Navitar’s ZOOM 7000-2 macro lens imaging system delivers superb optical performance and image quality for visible and SWIR imaging. Their robust design ensures reliability even in harsh environments. ZOOM 7000-2 macro lenses are ideal for applications, such as machine vision, scientific and medical imaging applications.

ZOOM 7000-2 VIS-SWIR lens – Courtesy Navitar

In fact there are three models in the series:

Each model has its application – but only the middle one is designed explicitly for VIS-SWIR – Courtesy Navitar

Kowa FC24M multispectral lenses

Kowa’s FC24M C-mount lens series are manufactured with wide-band multi-coating. That minimizes flare and ghosting from VIS through NIR. These lenses are also compelling for a number of other reasons, including wide working range (as close as 15 cm MOD), durable construction, and a unique close distance aberration compensation mechanism.

FC24M C-mount lens series – Courtesy Kowa

That “floating feature” creates stable optical performance at various working distances. Internal lens groups move independently of each other, which optimizes alignment compared to traditional lens design.

Tamron Wide-band SWIR lenses

Other lensing options include Tamron’s Wide-band SWIR lenses. While the name says SWIR, in fact they are VIS-SWIR. Designed for compatibility with Sony’s IMX990 and IMX991 SenSWIR sensors, you have even more lens choices. Call us at 978-474-0044 if you’d like us to help you navigate to best-fit components in cameras, lensing, and lighting, for your particular application.

1st Vision’s sales engineers have over 100 years of combined experience to assist in your camera and components selection. With a large portfolio of cameras, lenses, cables, NIC cards and industrial computers, we can provide a full vision solution!

About you: We want to hear from you! We’ve built our brand on our know-how and like to educate the marketplace on imaging technology topics… What would you like to hear about?… Drop a line to info@1stvision.com with what topics you’d like to know more about.

November 7, 2025

Kowa HC-V Ruggedized Lenses

Kowa HC-V 1″ C-mount industrial lenses feature a patented design that ensures dependable performance, and consistently clear, crisp images with uniform brightness across the entire image, including the corners. These ruggedized lenses are built for use in harsh environments to withstand strong vibrations and impacts.

Interchangeable iris plates and a two-way reversible nut enable precise focus adjustments, and glued inner glass elements ensure stability. HC-V lenses are compatible with 1″ format sensors including Sony IMX174, CMOSIS CMV4000, and Sony IMX249 sensors. Designed for sensors with a pixel size as small as 5.0μm.

HC-V ruggedized lens series – Courtesy Kowa

Choosing a sensor and matching a lens

If you’ve already chosen your sensor and camera, our knowledge base Guide to Key Considerations in Lens Selection may be helpful.

If you want to read about sensor selection, see our blog “Keys to Choosing the Best Image Sensor“.

Or for expert assistance just call us at 978-474-0044.

Interchangeable iris plates

The HC-V patented design includes interchangeable iris plates. Secured by a lock nut, this insures precise focus that’s vibration resistant. Ideal for rugged industrial environments.

HC-V ruggedized lens series overview – Courtesy Kowa

How to change the iris plates

How to change the iris plates – Courtesy Kowa

Happy to help

We’re pleased to distribute Kowa lenses, and to advise customers on all aspects of machine vision component selection. Whether for sensor, camera, lens, lighting, software, or other components, tell us about your application, and we’ll be happy to guide you to optimal choices. By phone we’re at 978-474-0044, or key in a few application notes below and we’ll reach out to you at your convenience.

June 30, 2025June 30, 2025

What can you see with a 67MP camera?

Remember when machine vision pioneers got stuff done with VGA sensors at 0.3MP? And the industry got really excited with 1MP sensors? Moore’s law keeps driving capacities and performance up, and relative costs down. With the Teledyne e2v Emerald 67MP sensor, cameras like the Genie Nano-10GigE-8200 open up new possibilities.

12MP sensor image – Courtesy Teledyne DALSA

67MP sensor image – Courtesy Teledyne DALSA

So what? 67MP view above right doesn’t appear massively compelling…

Well at this view, without zooming in, we’d agree….

But at 400% zoom, below, look at the pixelation differences:

Both images below show the same target region, with the same lighting and lens, and each zoomed (with Gimp) to 400%. There is so much pixelation in the 12MP image to raise doubts about effective edge detection on either the identifying digits (33) or for the metal-rimmed holes. Whereas the 67MP image has far less pixelation, thereby passing a readily usable image to the host for processing. How much resolution does your application require?

Important “aside”: Sensor format and lens quality also important

Sensor format refers to the physical size of the sensor and the pixel shape and pixel density. Of course the lens must physically mount to the camera body (e.g. S, C, M42, etc.), but it must also create an image circle that appropriately covers the sensor’s pixel array. The Genie Nano-10Gige-8200 uses the Teledyne e2V Emerald 67M packs just over 67 million pixels, each square pixel just 2.5 µm wide and high, onto a CMOS sensor measuring only 59mm x 59mm.

Consider other good quality cameras and sensors, with pixel sizes in the 4 – 5 µm range, which leads to EITHER fewer pixels overall in the same size sensor array; OR to a much larger sensor to accommodate more pixels. The former may limit what can be accomplished with a single camera. The latter would necessarily make the camera body larger, the lens mount larger, and the lens more expensive to manufacture.

The lens quality, typically expressed via the Modulation Transfer Function (MTF), is also important. Not all lenses are created equal! A “good” quality lens may be enough for certain applications. For more demanding applications, one would be wasting a large format sensor if the lens’ performance fails below the sensor’s capabilities.

Two different lenses were used to take the above images, both fitting the sensor size. However the right image was taken with a lens designed for smaller pixels versus the left. – Courtesy Teledyne DALSA

The high-level views of the test chart above tease at the point we’re making, but it really pops if we zoom in. Look at the difference in contrast in the two images below!

Lens nominally a fit for the sensor format and mount type, but NOT designed for 2.5 µm pixels.

The takeaway point of this segment is lensing matters! The machine vision field benefits users tremendously with segmented sensor, camera, lensing, and lighting suppliers. Even within the same supplier’s lineup, there are often sensors or lenses pitched at differing performance requirements. Consider our Knowledge Base guide on Lens Quality Considerations. Or call us at 978-474-0044.

Another example:

Below see the same concentric rings of a test chart, under the same lighting. The left imaged was obtained with a good 12MP sensor and good quality lens matched to the sensor format and pixel size. The right imaged used the 67MP sensor in the Genie-Nano-10GigE-8200, also with a well-matched lens.

If you need a single-camera solution for a large target, with high levels of detail, there’s no way around it – one needs enough pixels. Together with a well-suited lens.

Teledyne DALSA 10GigE Genie Nano — Genie Nano 10GigE 8200 – Courtesy Teledyne DALSA

The Genie Nano 10GigE 8200, in both monochrome and color versions, is more affordable than you might think.

Once more with feeling…

Which of the following images will lead to the more effective outcomes? Choose your sensor, camera, lens, and lighting accordingly. Call us at 978-474-0044. Our sales engineers love to create solutions for our customers.

June 4, 2025June 4, 2025

Collimated lighting important with telecentric lens

LTCLHP Collimated Light – Courtesy Opto Engineering

Machine vision practitioners, regardless of application or lens type, know that contrast is essential. Without sharp definition, features cannot be detected effectively.

When using a telecentric lens for precision optical 2-D measurements, ideally one should also use collimated lighting. Per the old adage about a chain being only as good as its weakest link, why invest in great lensing and then cut corners on lighting?

WITH collimated light expect high edge definition:

The cost of the light typically pays for itself relative to quality outcomes. Below see red-framed enlargements of the same region of a part being imaged by the same telecentric lens.

The left-hand image was taken with a conventional backlight – note how the light wraps around the edge, creating “confusion” and imprecision due to refracted light coming from all angles.

The right-hand image was obtained with a collimated backlight – with excellent edge definition.

Conventional backlight (left) vs. collimated backlight (right) – Courtesy Opto Engineering.

It all comes down to resolution

While telecentric imaging is a high-performance subset of the larger machine vision field in general, the same principles of resolution apply. It takes several pixels to confidently resolve any given feature – such as an edge – so any “gray areas” induced by lower quality lighting or optics would drag down system performance. See our blog and knowledge-base coverage of resolution for more details.

Collimated lighting in more detail

Above we see the results of using “diffuse” vs. “collimated” light sources, which are compelling. But what is a collimated light and how does it work so effectively?

UNLIKE a diffuse backlight, whose rays emanate towards the object at angles ranging from 0 to almost 180°, a collimated backlight sends rays with only very small deviations from perfectly parallel. Since parallel rays are also all that the telecentric lens receives and transmits on to the camera sensor, stray rays are mitigated and essentially eliminated.

The result is a high-contrast image which is easier to process with high-reliability. Furthermore, shutter speeds are typically faster, achieving necessary saturation more quickly, thereby shortening cycle times and increasing overall throughput.

Many lights to choose from:

The video below shows a range of light types and models, including clearly labeled direct, diffuse, and collimated lights.

Several light types – including clearly labeled collimated lights

[Optional] Telecentric concepts overview

Below please compare the diagrams that show how light rays travel from the target position on the left, through the respective lenses, and on to the sensor position on the far right.

A telecentric lens is designed to insure that the chief rays remain parallel to the optical axis. The key benefit is that (when properly focused and aligned) the system is invariant to the distance of the object from the lens. This effectively ignores light rays coming from other angles of incidence, and thereby supports precise optical measurement systems – a branch of metrology.

If you’d like to go deeper on telecentrics, see the following two resources:

Telecentric concepts presented as a short blog.

Alternatively as a more comprehensive Powerpoint from our KnowledgeBase.

Video: Selecting a telecentric lens:

Call us at 978-474-0044 to tell us more about your application – and how we can guide you through telecentric lensing and lighting options.